Concrete06

This command is used to construct a uniaxial concrete material object with tensile strength, nonlinear tension stiffening and compressive behavior based on Thorenfeldt curve.

Model.uniaxial(“Concrete06”,
name,
fc,
e0,
n,
k,
alpha1,
fcr,
ecr,
b,
alpha2)

`fc`	`float`	concrete compressive strength (compression is negative)*
`e0`	`float`	strain at compressive strength*
`n`	`float`	compressive shape factor
`k`	`float`	post-peak compressive shape factor
`alpha1`	`float`	\(\alpha_1\) parameter for compressive plastic strain definition
`fcr`	`float`	tensile strength
`ecr`	`float`	tensile strain at peak stress (`fcr`)
`b`	`float`	exponent of the tension stiffening curve
`alpha2`	`float`	\(\alpha_2\) parameter for tensile plastic strain definition

Notes:

Compressive concrete parameters should be input as negative values.

Examples

uniaxialMaterial Concrete06 1 -3 -0.002 2 1 0.32 0.3 0.00008 4 0.08

Discussion

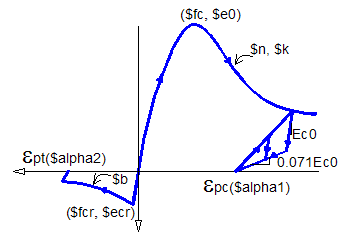
The concrete material, Concrete06 (Fig. 2), keeps the simplicity of previous formulations (Concrete01 to Concrete03). However, envelope curves have been modified to represent concrete behavior in membrane elements. Compressive constitutive material law (?c-?c) is defined as the Thorenfeldt-base curve, which is similar to Popovic (1973) definition:

\[ \sigma_c = f^\prime_c \frac{n \left(\frac{\epsilon_c}{\epsilon_0}\right)}{n-1 + \left( \frac{\epsilon_c}{\epsilon_0} \right)^{nk}} \]

where \(f^\prime_c\) is the compressive strength, \(\epsilon_0\) is the strain at peak compressive stress, and \(n\) and \(k\) are parameters.

The tensile envelope uses the tension stiffening equation by Belarbi and Hsu (1994) with a general exponent \(b\).

\[\epsilon_c \le \epsilon_{\text{cr}}, \sigma_c = \left( \frac{f_\text{cr}}{\epsilon_\text{cr}} \right) \epsilon_c\]

\[\epsilon_c \gt \epsilon_{\text{cr}}, \sigma_c = f_\text{cr} \left( \frac{\epsilon_\text{cr}}{\epsilon_\text{c}} \right)^b \]

where \(f_\text{cr}\) is the tensile strength, \(\epsilon_\text{cr}\) is the strain at tensile strength and \(b\) is a parameter.

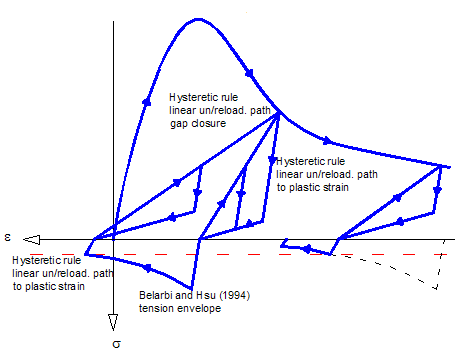
Hysteretic rules in compression are held similarly as defined in Concrete03, with linear unloading and reloading paths (constant stiffness). The unloading and reloading paths in compression are connected through unloading/reloading paths with initial elastic stiffness (Fig. 2 and 3). The unloading path in compression has a stiffness of \(7.1\%\) of the initial elastic stiffness (\(0.071E_c\)) as adopted by Palermo and Vecchio (2003). The plastic compressive strain \(\epsilon^p_c\)), defined as the residual unrecoverable compressive strain obtained after full unloading (zero stress) is characterized by:

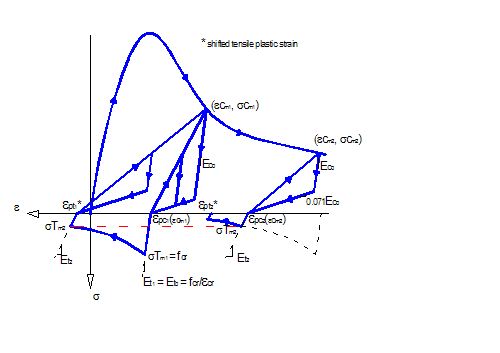
\[\epsilon^c_p = \epsilon^c_m \left( 1 - e ^{-\frac{\epsilon^c_m}{\epsilon_\text{cr}} \alpha_1} \right) \]

where \(\epsilon_m^c\)is the maximum (absolute value) compressive strain attained previously on the envelope (stored value by the uniaxial material), and \(\alpha_1\) is a parameter.

A origin-oriented hysteretic rule for tension may introduce inaccuracies in the analysis. In this case, stresses are linear and recover the initial strain (from previous cycle) when reducing to zero. However, after opening of cracks, under unloading from tension, the uneven and rough surface of the crack tend to initiate contact before the initial strain from previous cycle is attained. This effect known as gap closure improves the dissipating characteristic of the hysteretic rule, reducing the pinching. For this reason, the hysteretic rule for concrete in tension in this model considers a plastic strain (different from zero or the strain from previous cycle) such that when going from tensile stresses to compressive stresses the gap closure effect is modeled by a linear path. Such consideration requires also keeping track of previous stiffness and maximum tensile stress, and the previous tensile plastic strain. This is required, since when going in a posterior cycle from compressive stresses to tensile stresses the compressive plastic strain will become the new origin of the tensile behavior, creating a shifting in the stress-strain curve in tension (Fig. 3). From that strain a linear path will be followed using the previous unloading stiffness in tension until the previous attained maximum tensile stress is reached.

In tension, the unloading and reloading paths are the same, and are defined by the tensile plastic strain \((\epsilon_p^t)\). A similar equation is used to characterize the tensile plastic strain as in compression:

\[ \epsilon^t_p = \epsilon^t_m \left(1 - e^{-\frac{\epsilon^t_m}{\epsilon_\text{cr}} \alpha_2} \right) \]

where \(\epsilon_m^t\) is the maximum tensile strain attained previously on the envelope (stored value by the uniaxial material), and \(\alpha_2\) is a parameter.

Even though the equation for plastic strain (tension or compression) can be generally used, an internal checking is included in the model such that the unloading/reloading paths have as maximum stiffness the initial stiffness.

References

Popovics, S., 1973, “A Numerical Approach to the Complete Stress-Strain Curve of Concrete”, Cement and Concrete Research, V. 3, No. 4, pp. 583-599.
Belarbi, H. and Hsu, T.C.C., 1994, “Constitutive Laws of Concrete in Tension and Reinforcing Bars Stiffened by Concrete”, ACI Structural Journal, V. 91, No. 4, pp. 465-474.
Palermo, D., and Vecchio, F. J., 2003, “Compression Field Modeling of Reinforced Concrete Subjected to Reversed Loading: Formulation”, ACI Structural Journal, V. 100, No. 5, pp. 616 - 625.

Code developed by: Leo Massone, University of Chile