ConcreteCM

This command is used to construct a UniaxialMaterial ConcreteCM (Kolozvari et al., 2015), which is a uniaxial hysteretic constitutive model for concrete developed by Chang and Mander (1994). This model is a refined, rule-based, generalized, and non-dimensional constitutive model that allows calibration of the monotonic and hysteretic material modeling parameters, and can simulate the hysteretic behavior of confined and unconfined, ordinary and high-strength concrete, in both cyclic compression and tension (Figure 1). The model addresses important behavioral features, such as continuous hysteretic behavior under cyclic compression and tension, progressive stiffness degradation associated with smooth unloading and reloading curves at increasing strain values, and gradual crack closure effects. Details of the model are available in the report by Chang and Mander (1994).

Model.uniaxial(“ConcreteCM”,
   name,
   fpcc,
   epcc,
   Ec,
   rc,
   xcrn,
   ft,
   et,
   rt,
   xcrp)

fpcc	float	Compressive strength (f’c)
epcc	float	Strain at compressive strength (\(\epsilon^\prime_c\))
Ec	float	Initial tangent modulus (\(E_c\))
rc	float	Shape parameter in Tsai’s equation defined for compression (\(r_c\))
xcrn	float	Non-dimensional critical strain on compression envelope (\(\epsilon^-_{cr}\), where the envelope curve starts following a straight line)
ft	float	Tensile strength (\(f_t\))
et	float	Strain at tensile strength (\(\epsilon\)t)
rt	float	Shape parameter in Tsai’s equation defined for tension (\(r_t\))
xcrp	float	Non-dimensional critical strain on tension envelope (\(\epsilon^ _{cr}\), where the envelope curve starts following a straight line – large value [e.g., 10000] recommended when tension stiffening is considered)
gap	int	gap = 0, less gradual gap closure (default); gap = 1, more gradual gap closure

Figure 1. Hysteretic Constitutive Model for Concrete by Chang and Mander (1994)

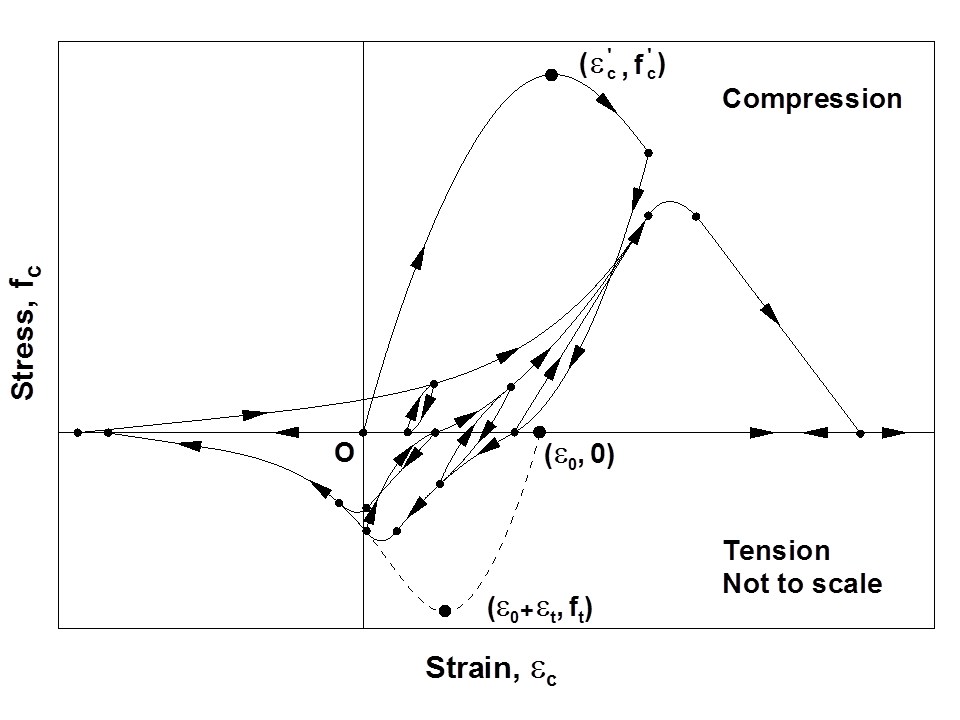
The Chang and Mander (1994) model generates continuous hysteretic stress-strain relationships with slope continuity for confined and unconfined concrete in both compression and tension. The compression envelope curve of the model is defined by the initial tangent slope, (E_c), the peak coordinate (\(\epsilon^\prime_c\), \(f^\prime_c\)), a parameter (r_c) from Tsai’s (1988) equation defining the shape of the envelope curve, and a parameter (\(\epsilon\)^-_cr) to define normalized (with respect to \(\epsilon^\prime_c\)) strain where the envelope curve starts following a straight line, until zero compressive stress is reached at the spalling strain, \(\epsilon_{sp}\). These parameters can be controlled based on specific experimental results for a refined calibration of the compression envelope (Figure 2). Chang and Mander (1994) proposed empirical relationships for parameters \(E_c\), \(\epsilon\)’_c, and r_c for unconfined concrete with compressive strength f’_c, based on review of previous research. Parameters f’_c, \(\epsilon\)’_c, E_c, r_c, and \(\epsilon\)^-_cr can also be calibrated to represent the stress-strain behavior of confined concrete in compression, to follow the constitutive relationships for confined concrete proposed by Mander et al (1988) or similar.

Figure 2. Compression and Tension Envelope Curves

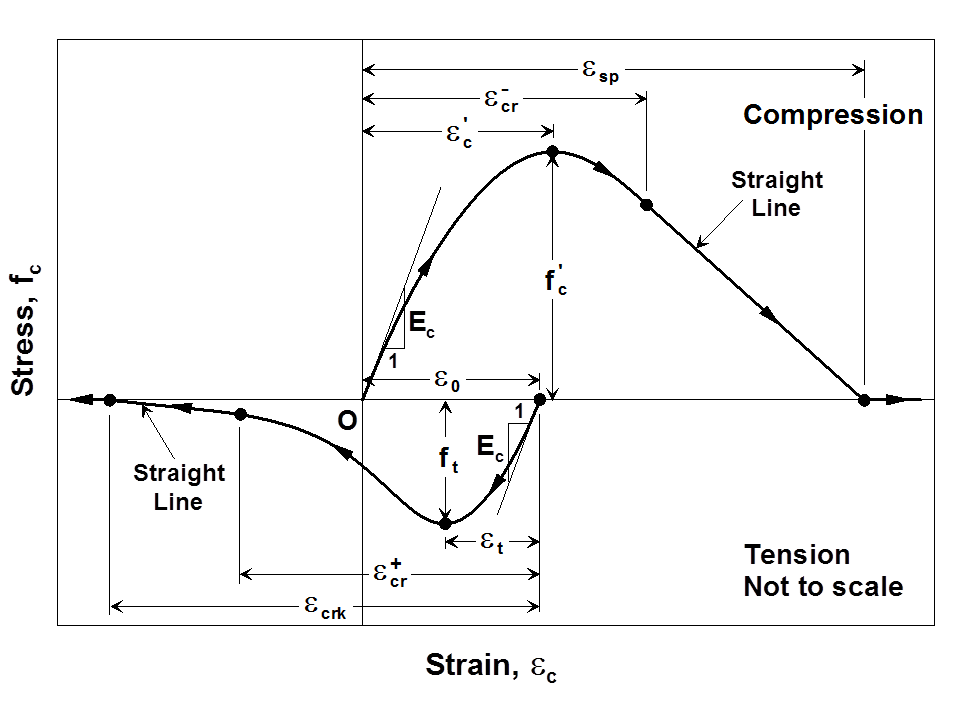
The shape of the tension envelope curve in the model is the same as that of the compression envelope; however, the tension envelope curve is shifted to a new origin that is based on the unloading strain from the compression envelope (Figure 2). As well, the strain ductility experienced previously on the compression envelope is also reflected on the tension envelope. The parameters associated with the tension envelope curve include the tensile strength of concrete (f_t), the monotonic strain at tensile strength ( \(\epsilon_\textrm{t}\) ), a parameter (r_t) from Tsai’s (1988) equation defining the shape of the tension envelope curve, and a parameter (\(\epsilon\)⁺_cr) to define normalized (with respect to \(\epsilon\)_t) strain where the tension envelope curve starts following a straight line, until zero tensile stress is reached at a strain of \(\epsilon\)_crk. These parameters can also be controlled and calibrated based on specific experimental results or empirical relations proposed by other researchers (e.g., Belarbi and Hsu, 1994) to model the behavior of concrete in tension and the tension stiffening phenomenon. Concrete experiencing tension stiffening can be considered not to crack completely; that is, a large value for parameter \(\epsilon\)⁺_cr (e.g., 10000) can be defined.

Source: /usr/local/cvs/OpenSees/SRC/material/uniaxial/

---

Input Format:

---

Example:

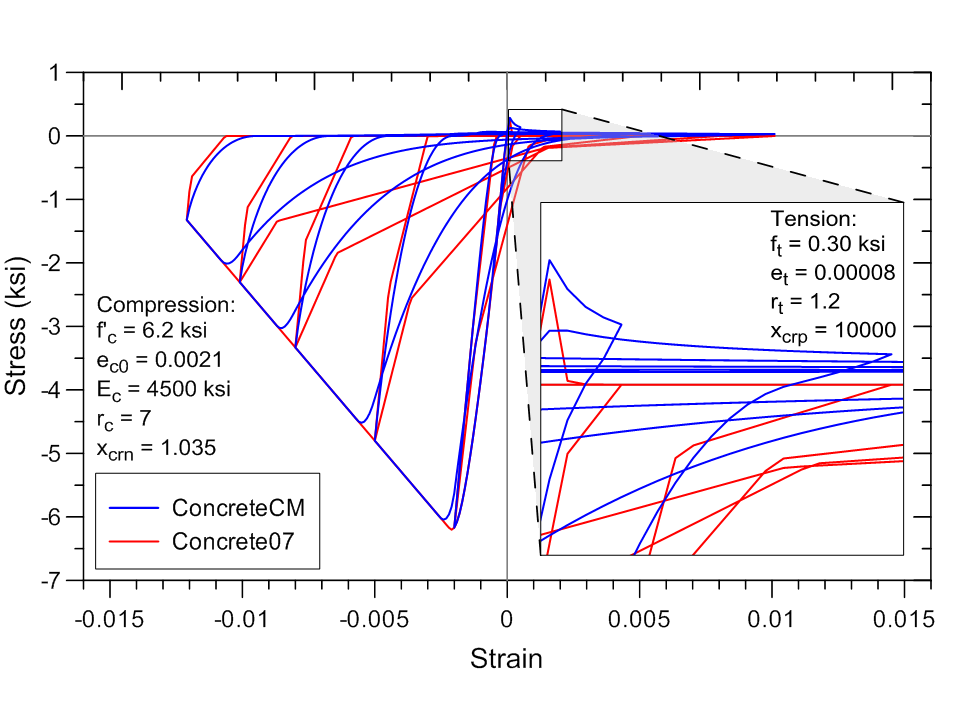
uniaxialMaterial ConcreteCM 1 -6.2 -0.0021 4500 7 1.035 0.30 0.00008 1.2 10000

Example of hysteretic stress-strain history generated by the model code is illustrated in Figure 3.

Figure 3. Concrete Stress-Strain Behavior

---

Discussion:

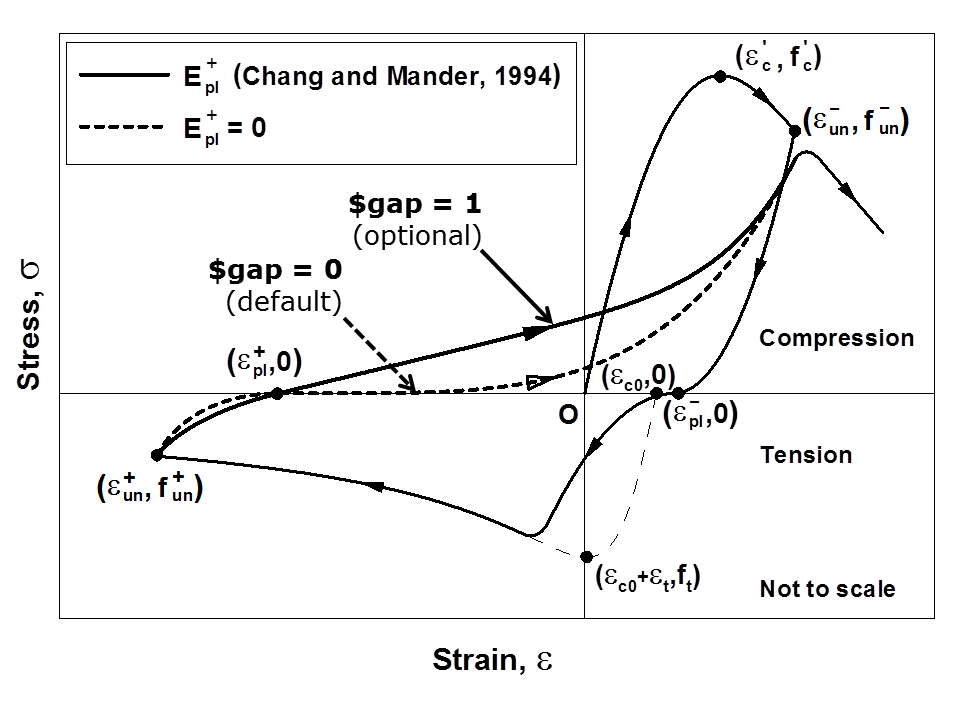
An optional input parameter gap is introduced in the ConcreteCM model implemented in OpenSees for providing the users with the opportunity to control the intensity of gap closure in the stress-strain behavior of concrete, which in-turn influences the level of pinching in the lateral load-displacement behavior of a RC wall. The original Chang and Mander (1994) model adopts a non-zero tangent stiffness at zero stress level upon unloading from the tension envelope, which is represented by gap = 1 in ConcreteCM. Using gap = 0 (default) produces less gradual gap closure, since it assumes zero tangent stiffness at zero stress level upon unloading from the tension envelope, and is suitable for most analyses. Figure 4 illustrates the effect of plastic stiffness upon unloading from tension envelope ( E⁺_pl) on crack closure, i.e. use of more gradual (gap = 1) or less gradual (gap = \(0\)) gap closure. The effect of parameter gap on predictions of flexural behavior of a RC wall is illustrated in Example 1 of MVLEM element.

Figure 4. Effect of Plastic Stiffness upon Unloading from Tension Envelope (Epl+) on Crack Closure

Constitutive stress-strain concrete behavior is also implemented in OpenSees in uniaxialMaterial Cocnrete07. However, ConcreteCM incorporates sophisticated unloading/reloading rules defined originally by Chang and Mander (1994), as opposed to Concrete07 that adopts simplified hysteretic rules. Comparison between stress-strain response predicted using ConcreteCM and Concrete07 is shown in Figure 5.

Figure 5. Comparison of ConcreteCM and Concrete07

---

References

• Belarbi H. and Hsu T.C.C. (1994), “Constitutive Laws of Concrete in Tension and Reinforcing Bars Stiffened by Concrete”, ACI Structural Journal, V. 91, No. 4, pp. 465-474.
• Chang, G.A. and Mander, J.B. (1994), “Seismic Energy Based Fatigue Damage Analysis of Bridge Columns: Part I - Evaluation of Seismic Capacity”, NCEER Technical Report No. NCEER-94-0006, State University of New York, Buffalo.
• Kolozvari K., Orakcal K., and Wallace J. W. (2015). “Shear-Flexure Interaction Modeling of reinforced Concrete Structural Walls and Columns under Reversed Cyclic Loading”, Pacific Earthquake Engineering Research Center, University of California, Berkeley, PEER Report No. 2015/12
• Mander J.B., Priestley M.J.N., and Park R. (1988). “Theoretical Stress-Strain Model for Confined Concrete”, ASCE Journal of Structural Engineering, V. 114, No. 8, pp. 1804-1826.
• Orakcal K.(2004), “Nonlinear Modeling and Analysis of Slender Reinforced Concrete Walls”, PhD Dissertation, Department of Civil and Environmental Engineering, University of California, Los Angeles.
• Tsai W.T. (1988), “Uniaxial Compressional Stress-Strain Relation of Concrete”, ASCE Journal of Structural Engineering, V. 114, No. 9, pp. 2133-2136.

Code developed by:

Kristijan Kolozvari , California State University, Fullerton

Kutay Orakcal, Bogazici University, Istanbul, Turkey

John Wallace, Univeristy of California, Los Angeles