ConfinedConcrete01

This command is used to construct an uniaxial material object of confined concrete in according to the work of Braga, Gigliotti and Laterza (2006). The confined concrete model (BGLmodel) has not tensile strength and degraded linear unloading/reloading stiffness as proposed by Karsan and Jirsa (1969). The BGL model accounts for confinement effects due to different arrangements of transverse reinforcement and/or external strengthening such as steel jackets or FRP wraps. The confinement effect along the column is described as well. In order to obtain th ecompressive envelope curve a non linear approach is performed at each increment of column axial strain.The sougth curve is obtained crossing different stress‐strain relationships, each of which corresponding to a different level of confinement. Currently, the Attard and Setunge’s model is implemented in calculating each active curve of the confined concrete. IMPORTANT: the units to be used are MPa, mm.

Model.uniaxial(“ConfinedConcrete01”,
   name,
   secType,
   fpc,
   E,
   eps_ult,
   poisson,
   L1,
   phis,
   S,
   fyh,
   Es0,
   haRatio,
   mu,
   phiLon)

secType str label for the transverse reinforcement configuration.
S1 square section with S1 type of transverse reinforcement with or without external FRP wrapping
S2 square section with S2 type of transverse reinforcement with or without external FRP wrapping
S3 square section with S3 type of transverse reinforcement with or without external FRP wrapping
S4a square section with S4a type of transverse reinforcement with or without external FRP wrapping
S4b square section with S4b type of transverse reinforcement with or without external FRP wrapping
S5 square section with S5 type of transverse reinforcement with or without external FRP wrapping
C circular section with or without external FRP wrapping
R rectangular section with or without external FRP wrapping.
fpc float
E float Young’s modulus of elasticity
eps_ult Alt
poisson Alt
L1 float length/diameter of square/circular core section measured respect to the hoop center line.
L2 float additional dimensions when multiple hoops are being used.
L3 float additional dimensions when multiple hoops are being used.
phis float hoop diameter. If section arrangement has multiple hoops it refers to the external hoop.
S float hoop spacing.
fyh float yielding strength of the hoop steel.
Es0 float elastic modulus of the hoop steel.
haRatio float hardening ratio of the hoop steel.
mu float ductility factor of the hoop steel.
phiLon float diameter of longitudinal bars.
internals [phisi,Si,fyhi,Es0i,haRatioi,mui], optional parameters for defining the internal transverse reinforcement.If they are not specified they will be assumed equal to the external ones (for S2, S3, S4a, S4b and S5 typed).
phisi float
Si float
fyhi float
Es0i float
haRatioi float
mui float
wrap [cover,Am,Sw,ful,Es0w],
cover float cover thickness measured from the outer line of hoop.
Am float total area of FRP wraps (number of layers x wrap thickness x wrap width).
Sw float spacing of FRP wraps (if continuous wraps are used the spacing is equal to the wrap width).
ful float ultimate strength of FRP wraps.
Es0w float elastic modulus of FRP wraps.
gravel = False bool
silica = False bool
tol float
maxNumIter float
epscuLimit float
stRatio float 
uniaxialMaterial ConfinedConcrete01 $tag $secType $fpc $Ec 
  ( < -epscu $epscu >  OR  < -gamma $gamma > ) 
  ( < -nu $nu >  OR < -varub >  OR  < -varnoub > ) $L1 ($L2) ($L3) $phis $S $fyh $Es0
  $haRatio $mu $phiLon  
  < -internal $phisi $Si $fyhi $Es0i $haRatioi $mui >
  < -wrap $cover $Am $Sw $fuil $Es0w >
  < -gravel > < -silica > < -tol $tol > < -maxNumIter $maxNumIter > 
  < -epscuLimit $epscuLimit > < -stRatio $stRatio >
matTag (int) integer tag identifying material
secType (str)

tag for the transverse reinforcement configuration. see image below.

  • ‘S1’ square section with S1 type of transverse reinforcement with or without external FRP wrapping
  • ‘S2’ square section with S2 type of transverse reinforcement with or without external FRP wrapping
  • ‘S3’ square section with S3 type of transverse reinforcement with or without external FRP wrapping
  • ‘S4a’ square section with S4a type of transverse reinforcement with or without external FRP wrapping
  • ‘S4b’ square section with S4b type of transverse reinforcement with or without external FRP wrapping
  • ‘S5’ square section with S5 type of transverse reinforcement with or without external FRP wrapping
  • ‘C’ circular section with or without external FRP wrapping
  • ‘R’ rectangular section with or without external FRP wrapping.
fpc (float) unconfined cylindrical strength of concrete specimen.
Ec (float) initial elastic modulus of unconfined concrete.
epscu_type (str) Method to define confined concrete ultimate strain - -epscu then value is confined concrete ultimate strain, - -gamma then value is the ratio of the strength corresponding to ultimate strain to the peak strength of the confined concrete stress-strain curve. If gamma cannot be achieved in the range [0, epscuLimit] then epscuLimit (optional, default: 0.05) will be assumed as ultimate strain.
epscu_val (float) Value for the definition of the concrete ultimate strain
nu (str) or (list) Definition for Poisson’s Ratio. - [‘-nu’, <value of Poisson’s ratio>] - ‘-varub’ Poisson’s ratio is defined as a function of axial strain by means of the expression proposed by Braga et al. (2006) with the upper bound equal to 0.5 -‘-varnoub’ Poisson’s ratio is defined as a function of axial strain by means of the expression proposed by Braga et al. (2006) without any upper bound.
L1 (float) length/diameter of square/circular core section measured respect to the hoop center line.
L2 (float) additional dimensions when multiple hoops are being used.
L3 (float) additional dimensions when multiple hoops are being used.
phis (float) hoop diameter. If section arrangement has multiple hoops it refers to the external hoop.
S (float) hoop spacing.
fyh (float) yielding strength of the hoop steel.
Es0 (float) elastic modulus of the hoop steel.
haRatio (float) hardening ratio of the hoop steel.
mu (float) ductility factor of the hoop steel.
phiLon (float) diameter of longitudinal bars.
internalArgs (list (float)) internalArgs= [phisi, Si, fyhi, Es0i, haRatioi, mui] optional parameters for defining the internal transverse reinforcement. If they are not specified they will be assumed equal to the external ones (for S2, S3, S4a, S4b and S5 typed).
wrapArgs (list (float))

wrapArgs=[cover, Am, Sw, ful, Es0w] optional parameters required when section is strengthened with FRP wraps.

  • cover cover thickness measured from the outer line of hoop.
  • Am total area of FRP wraps (number of layers x wrap thickness x wrap width).
  • Sw spacing of FRP wraps (if continuous wraps are used the spacing is equal to the wrap width).
  • ful ultimate strength of FRP wraps.
  • Es0w elastic modulus of FRP wraps.
‘-gravel’ (str) Unknown
‘-silica’ (str) Unknown
tol (float) Unknown
maxNumIter (int) Unknown
epscuLimit (float) Unknown
stRatio Unknown
tag

integer tag identifying material.

secType

tag for the transverse reinforcement configuration. See NOTE 1.

fpc

unconfined cylindrical strength of concrete specimen.

Ec

initial elastic modulus of unconfined concrete.

<-epscu $epscu> OR <-gamm $gamma>

confined concrete ultimate strain. See NOTE 2.

<-nu \(nu&gt; OR &lt;-varub&gt; OR &lt;-varnoub&gt;</strong></p></td> <td><p>Poisson's Ratio. See NOTE 3.</p></td> </tr> <tr class="odd"> <td><p><code class="parameter-table-variable">L1</code></p></td> <td><p>length/diameter of square/circular core section measured respect to the hoop center line.</p></td> </tr> <tr class="even"> <td><p><strong>(\)L2), ($L3)

additional dimensions when multiple hoops are being used. See NOTE 4.

phis

hoop diameter. If section arrangement has multiple hoops it refers to the external hoop.

S

hoop spacing.

fyh

yielding strength of the hoop steel.

Es0

elastic modulus of the hoop steel.

haRatio

hardening ratio of the hoop steel.

mu

ductility factor of the hoop steel.

phiLon

diameter of longitudinal bars.

<-internal $phisi $Si $fyhi $Es0i $haRatioi $mui>

optional parameters for defining the internal transverse reinforcement. If they are not specified they will be assumed equal to the external ones (for S2, S3, S4a, S4b and S5 typed).

<-wrap $cover $Am $Sw $ful $Es0w>

optional parameters required when section is strengthened with FRP wraps. See NOTE 5.

NOTES:

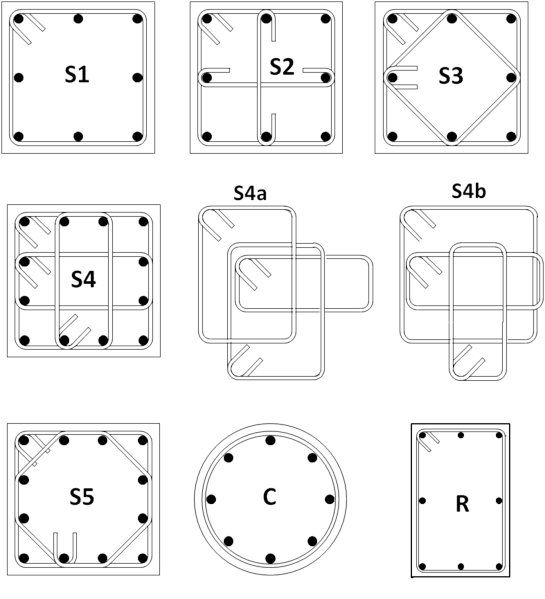
  1. The following section types are available:

    S1

    square section with S1 type of transverse reinforcement with or without external FRP wrapping;

    S2

    square section with S2 type of transverse reinforcement with or without external FRP wrapping;

    S3

    square section with S3 type of transverse reinforcement with or without external FRP wrapping;

    S4a

    square section with S4a type of transverse reinforcement with or without external FRP wrapping;

    S4b

    square section with S4b type of transverse reinforcement with or without external FRP wrapping;

    S5

    square section with S5 type of transverse reinforcement with or without external FRP wrapping;

    C

    circular section with or without external FRP wrapping;

    R

    rectangular section with or without external FRP wrapping.

    SectionTypes.png

    1. The confined concrete ultimate strain is defined using -epscu or -gamma. When -gamma option is specified, gamma is the ratio of the strength corresponding to ultimate strain to the peak strength of the confined concrete stress-strain curve. If gamma cannot be achieved in the range [0, epscuLimit] then epscuLimit (optional, default: 0.05) will be assumed as ultimate strain.

      1. Poisson’s Ratio is specified by one of these 3 methods: a) providing nu using the -nu option. b) using the -varUB option in which Poisson’s ratio is defined as a function of axial strain by means of the expression proposed by Braga et al. (2006) with the upper bound equal to 0.5; or c) using the -varNoUB option in which case Poisson’s ratio is defined as a function of axial strain by means of the expression proposed by Braga et al. (2006) without any upper bound.

        1. L1 (2l), L2 (a) and L3 (b) are required when either S4a or S4b section types is used. L1 (2d) and L2 (2c) must be used for rectangular section.

          1. When external stengthening is used must be specified the following parameters:

cover

cover thickness measured from the outer line of hoop.

Am

total area of FRP wraps (number of layers x wrap thickness x wrap width).

Sw

spacing of FRP wraps (if continuous wraps are used the spacing is equal to the wrap width).

ful

ultimate strength of FRP wraps.

Es0w

elastic modulus of FRP wraps.

  1. Stresses and strains can be defined either as positive or as negative values. All commands are not case sensitive.

Examples

Square section reinforced by simple transverse hoop and by additional FRP wraps (Section S1)

S1.png

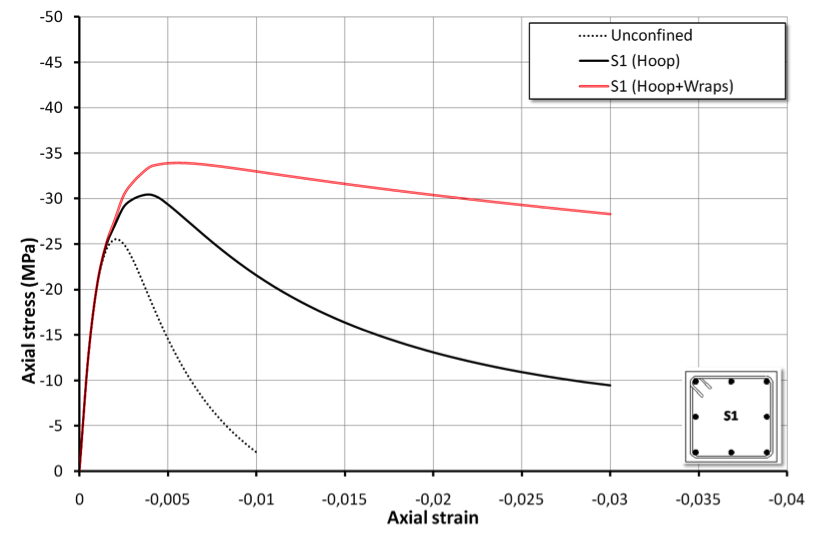
Section S1 

# uniaxialMaterial ConfinedConcrete01 $tag $secType $fpc $Ec -epscu
#        $epscu $nu $L1 $phis $S $fyh $Es0 $haRatio $mu $phiLon -stRatio
#        $stRatio</li>

uniaxialMaterial ConfinedConcrete01 1 S1 -30.0 26081.0 -epscu -0.03 \
  -varub 300.0 10.0 100.0 300.0 206000.0 0.0 1000.0 16.0 -stRatio 0.85

Section S1 strengthened by additional FRP wraps

# uniaxialMaterial ConfinedConcrete01 $tag $secType $fpc $Ec -epscu
#        $epscu $nu $L1 $phis $S $fyh $Es0 $haRatio $mu phiLon $cover $Am $Sw
#        $ful $Es0w -stRatio $stRatio</li>


uniaxialMaterial ConfinedConcrete01 1 S1 -30.0 26081.0 -epscu -0.03 \
  -varub 300.0 10.0 100.0 300.0 206000.0 0.0 1000.0 16.0 \
  -wrap 30.0 51.0 100.0 3900.0 230000.0 -stRatio 0.85

Square section reinforced by multiple transverse hoop and by additional FRP wraps (Section S4a)

S4a.png

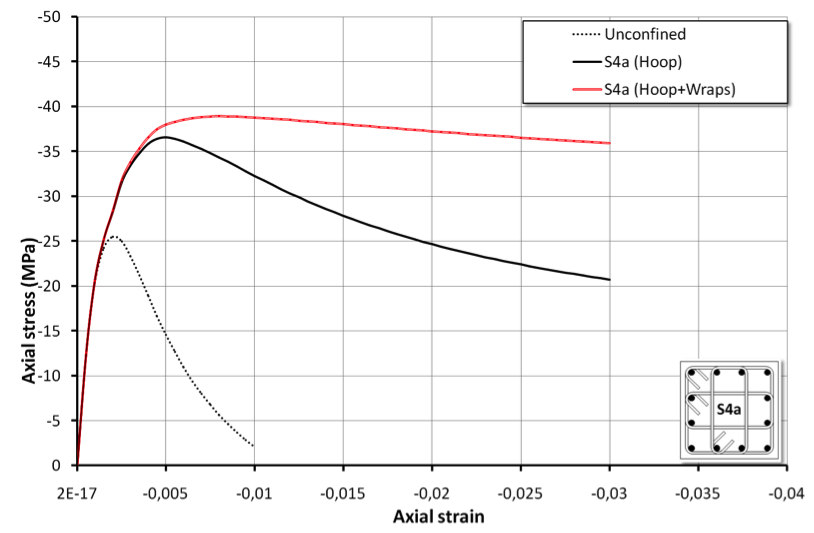
Section S4a

# uniaxialMaterial ConfinedConcrete01 $tag $secType $fpc $Ec -epscu
#     $epscu $nu $L1 $L2 $L3 $phis $S $fyh $Es0 $haRatio $mu $phiLon -stRatio
#     $stRatio</li>

uniaxialMaterial ConfinedConcrete01 1 S4a -30.0 26081.0 -epscu -0.03 \
    -varUB 300.0 200.0 100.0 10.0 100.0 300.0 206000.0 0.0 1000.0 16.0 \
    -stRatio 0.85

Section S4a strengthened by additional FRP wraps

# uniaxialMaterial ConfinedConcrete01 $tag $secType $fpc $Ec -epscu
#        $epscu $nu $L1 $L2 $L3 $phis $S $fyh $Es0 $haRatio $mu $phiLon $cover
#        $Am $Sw $ful $Es0w -stRatio $stRatio

uniaxialMaterial ConfinedConcrete01 1 S4a -30.0 26081.0 -epscu -0.03 \
        -varUB 300.0 200.0 100.0 10.0 100.0 300.0 206000.0 0.0 1000.0 16.0 \
        -wrap 30.0 51.0 100.0 3900.0 230000.0 -stRatio 0.85

Rectangular section reinforced by simple transverse hoop and by additional FRP wraps (Section R)

R.png

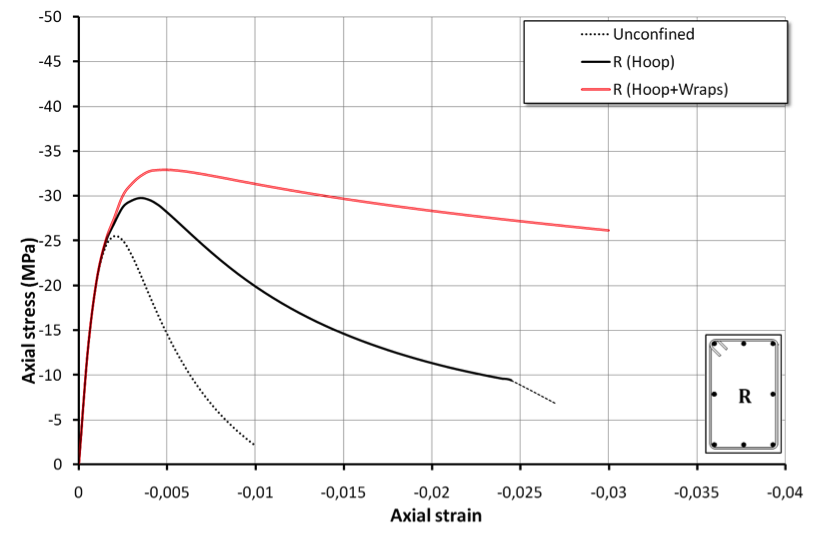
Section R 

# uniaxialMaterial ConfinedConcrete01 $tag $secType $fpc $Ec -epscu $epscu $nu $L1 $L2 $phis $S $fyh $Es0 $haRatio $mu $phiLon -stRatio $stRatio

uniaxialMaterial ConfinedConcrete01 1 R -30.0 26081.0 -epscu -0.03 \
  -varUB 500.0 300.0 10.0 100.0 300.0 206000.0 0.0 1000.0 16.0  \
  -stRatio 0.85

Section R strengthened by additional FRP wraps


# uniaxialMaterial ConfinedConcrete01 $tag $secType $fpc $Ec -epscu \
#   $epscu $nu $L1 $L2 $phis $S $fyh $Es0 $haRatio $mu $phiLon $cover $Am \
#   $Sw $ful $Es0w -stRatio $stRatio

uniaxialMaterial ConfinedConcrete01 1 R -30.0 26081.0 -epscu -0.03 \
  -varUB 500.0 300.0 10.0 100.0 300.0 206000.0 0.0 1000.0 16.0 -wrap 30.0 \
  51.0 100.0 3900.0 230000.0 -stRatio 0.85

REFEERENCES:

  1. Attard, M. M., Setunge, S., 1996. “Stress-strain relationship of confined and unconfined concrete”. Material Journal ACI, 93(5), 432-444
  2. Braga, F., Gigliotti, R., Laterza, M., 2006. “Analytical stress-strain relationship for concrete confined by steel stirrups and/or FRP jackets”. Journal of Structural Engineering ASCE, 132(9), 1402-1416.
  3. D’Amato M., February 2009. “Analytical models for non linear analysis of RC structures: confined concrete and bond-slips of longitudinal bars”. Doctoral Thesis. University of Basilicata, Potenza, Italy.
  4. D’Amato, M., Braga, F., Gigliotti, R., Kunnath S., Laterza, M., 2012. “A numerical general-purpose confinement model for non-linear analysis of R/C members”. Computers and Structures Journal, Elsevier, Vol. 102-103, 64-75.
  5. Karsan, I. D., Jirsa, J. O., 1969. “Behavior of concrete under compressive loadings”, Journal of Structural Division ASCE, 95(12), 2543-2563.

Code Developed by: Michele D’Amato, University of Basilicata, Italy