QzSimple1

This command is used to construct a QzSimple1 uniaxial material.

Model.uniaxial(“QzSimple1”, name, qzType, qult, Z50)

qzType

str

1	Backbone of $q-z$ curve approximates Reese and O’Neill’s (1987) relation for drilled shafts in clay.
2	Backbone of $q-z$ curve approximates Vijayvergiya’s (1977) relation for piles in sand.

qult float Ultimate capacity of the $q-z$ material. SEE NOTE 1.

Z50 float Displacement at which 50% of qult is mobilized in monotonic loading. SEE NOTE 2.

suction float Uplift resistance is equal to suctionqult. Default = 0.0. The value of suction must be 0.0 to 0.1.

c float The viscous damping term (dashpot) on the far-field (elastic) component of the displacement rate (velocity). Default = 0.0. Nonzero c values are used to represent radiation damping effects.*

NOTES:

qult: Ultimate capacity of the $q$-$z$ material. Note that “q” or “qult” are stresses [force per unit area of pile tip] in common design equations, but are both loads for this uniaxialMaterial [i.e., stress times tip area].
Y50: Displacement at which 50% of pult is mobilized in monotonic loading. Note that Vijayvergiya’s relation (qzType=2) refers to a “critical” displacement (zcrit) at which qult is fully mobilized, and that the corresponding z50 would be 0. 125zcrit.
optional args $suction and $c must either both be omitted or both provided.

EQUATIONS and EXAMPLE RESPONSES:

The equations describing QzSimple1 behavior are similar to those for $p$-$y$ materials by Boulanger, R. W., Curras, C. J., Kutter, B. L., Wilson, D. W., and Abghari, A. (1999). “Seismic soil-pile-structure interaction experiments and analyses.” Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 125(9): 750-759.

Modifications were required for representing the different responses of a $q-z$ material in compression versus uplift.

The nonlinear $q$-$z$ behavior is conceptualized as consisting of elastic ($q$- $z^e$ ), plastic $z^e$ ) $z^e$ ) ($q$-$z^p$), and gap ($q-z^g$) components in series. Radiation damping is modeled by a dashpot on the “far-field” elastic component ( $q-z^e$ ) of the displacement rate. The gap component consists of a bilinear closure spring ( $q^c-z^g$ ) in parallel with a nonlinear drag $q^c-z^g$ ) spring ($q^d-z^g$). Note that $z = z^e + z^p + z^g$ , and that $q = q^d + q^c$ .

The plastic component has an initial range of rigid behavior between

\[-C_r q_\text{ult} < q < C_r q_\text{ult}\]

with $C_r$ = the ratio of $\frac{q}{q_{\text{ult}}}$ when plastic yielding first occurs in virgin loading. The rigid range of $q$, which is initially $2 C_r q_\text{ult}$ , translates and grows with plastic yielding. The rigid range of $q$ is constrained to a maximum size of $0.7q_{\text{ult}}$. Beyond the rigid range, loading of the plastic ( $q-z^p$ ) component is described by:

\[q = q_{\text{ult}} - (q_{\text{ult}} - q_0) \left [\frac{c * z_{50}}{c * z_{50} + | z_p - z^p_0|} \right ]\]

where $q_\textrm{ult}$ = the ultimate resistance of the $q-z$ material in the current loading direction, $q_o = q$ at the start of the current plastic loading cycle, p $z^p_o = z^p$ at the start of the current plastic loading cycle, and c and n are constants that control the shape of $q-z^p$ curve.

The closure ( $q^c-z^g$ ) component is simply a bilinear elastic spring, which is relatively rigid in compression and extremely flexible in tension (uplift).

The nonlinear drag ( $q^d-z^g$ ) component is used to allow thethe specification of some minimum “suction” on the pile tip during uplift. It is described by:

\[q^d = C_d q_\text{ult} - (C_d q_{\text{ult}} - q^d_0) \left [\frac{z_{50}}{z_{50} + 2| z^g - z^g_0|} \right ] \]

where $C_d$ = ratio of the maximum drag (suction) force to the ultimate resistance of the $q-z$ material, $q^d_o = q^d$ at the start of the current loading cycle, and $z^g_o = z^g$ at the start of the current loading cycle.

The flexibility of the above equations can be used to approximate different q-z backbone relations. Reese and O’Neill’s (1987) recommended backbone for drilled shafts in clay is closely approximated using $c = 0.35$, $n = 1.2$, and $C_r = 0.2$ . Vijayvergiya’s (1977) recommended backbone for piles in sand is closely approximated using $c = 12.3$, $n = 5.5$, and $C_r = 0.3$ .

QzSimple1 is currently implemented to allow use of these two default sets of values. Values of $q_\text{ult}$, $z_50$ , and suction (i.e., $C_d$ ) must then be specified to define the $q-z$ material behavior.

Viscous damping on the far-field (elastic) component of the $q-z$ material is included for approximating radiation damping. For implementation in OpenSees the viscous damper is placed across the entire material, but the viscous force is calculated as proportional to the component of velocity (or displacement) that developed in the far-field elastic component of the material. For example, this correctly causes the damper force to become zero during load increments across a fully formed gap in uplift. In addition, the total force across the $q-z$ material is restricted to $q_\text{ult}$ in magnitude so that the viscous damper cannot cause the total force to exceed the near-field soil capacity. Users should also be familiar with numerical oscillations that can develop in viscous damper forces under transient loading with certain solution algorithms and damping ratios. In general, an HHT algorithm is preferred over a Newmark algorithm for reducing such oscillations in materials like QzSimple1.

Examples of the monotonic backbones and cyclic loading response of QzSimple1 are given in the following plots.

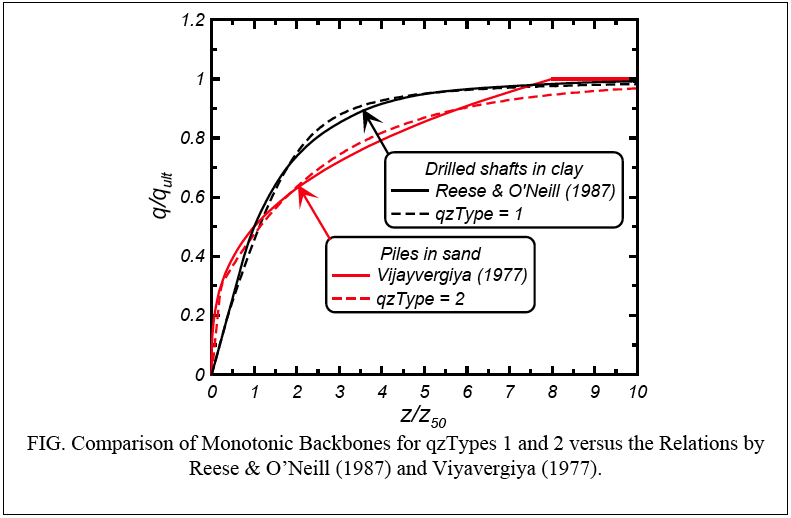
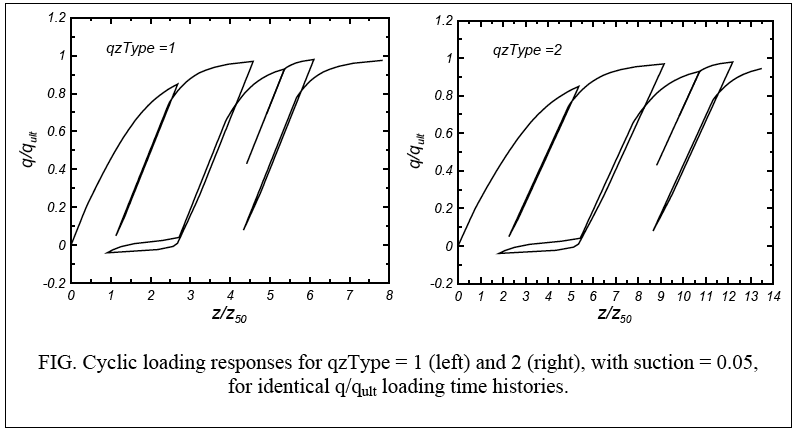
Examples

References

“Seismic Soil-pile-strcture interaction experiments and analysis”, Boulanger, R.W., Curras, C.J., Kutter, B.L., Wilson, D.W., and Abghari, A. (1990). Jornal of Geotechnical and Geoenvironmental Engineering, ASCS, 125(9):750-759.

Code Developed by: Ross Boulanger, UC Davis